학생시절 배웠던 다각형의 면적구하기를 코딩으로 만나보면
새롭지 않을까? 라는 생각으로 문제를 고르게 되었다.
Baekjoon / Problem No. 2166 (다각형의 면)
Problem
2차원 평면상에 N(3 ≤ N ≤ 10,000)개의 점으로 이루어진 다각형이 있다. 이 다각형의 면적을 구하는 프로그램을 작성하시오.
Input
첫째 줄에 N이 주어진다. 다음 N개의 줄에는 다각형을 이루는 순서대로 N개의 점의 x, y좌표가 주어진다. 좌표값은 절댓값이 100,000을 넘지 않는 정수이다.
Output
첫째 줄에 면적을 출력한다. 면적을 출력할 때에는 소수점 아래 둘째 자리에서 반올림하여 첫째 자리까지 출력한다.
Solution 1
우선 아이디어 자체는 그리 새로운 것을 필요로 하지 않는다. 다만 몇몇 수학 공식들을 알고있으면 굉장히 편하게 풀 수 있는 문제였다.
각 점의 좌표를 모두 아는 평면상의 다각형의 넓이를 구하는 방법의 시작은
중,고등학교 과정에서 배우는 바로는(정확히 기억나지는 않는다.) 기본적으로 "삼각형으로 나누기" 이다.

다음과 같은 오각형은 3개의 삼각형으로 잘라서 각각의 넓이를 구한다.
각각의 삼각형의 넓이를 구하는 방법은 중, 고등학생들도 익히 들어봤을 법한 '헤론의 공식'을 이용한다.

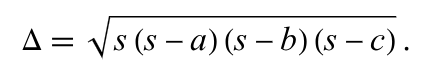
여기서 S는 삼각형의 둘레이며, 아래의 식은 삼각형의 넓이를 나타낸다. 기본적으로 삼각형으로 쪼갠 후, 헤론의 공식을 이용하여 다각형의 널이를 구하는 방법이 있다.
헤론의 공식이 궁금한 수학쟁이가 있다면 https://mathworld.wolfram.com/HeronsFormula.html 이곳을 참고하자.
(사이트 이름부터 수학세상이다.)
다각형의 종류에는 여러가지가 있는데, 모양을 기준으로 나누어 보면 "볼록"한 것과 "오목"한 것으로 나뉜다.
헤론의 공식 등을 이용하여 삼각형을 나누는 경우에 볼록 다각형은 크게 문제가 없지만, 오목 다각형의 경우 오목한 부분이 많아지면 모양에 따라 계산이 더 복잡해지고, 머리가 아파오기 시작한다.

하지만 삼각형으로 쪼개고 둘레를 구하고 넓이를 구하는 방법은 복잡하고, 정제되어 있지 않다. (아름답지 않다.)
다각형의 넓이를 하나의 공식으로 뚝딱하고 풀 수는 없을까? "짜잔, 그것이 실제로 있었습니다."
이것 역시 일부 중, 고등학생들이 들어봤을 법한 '가우스 면적 공식 = 사선정리 = 신발끈 공식' 이다.

행렬의 개념이 포함되어 있는데 대부분의 학생들은 이 사진이 더 익숙할 것이다.
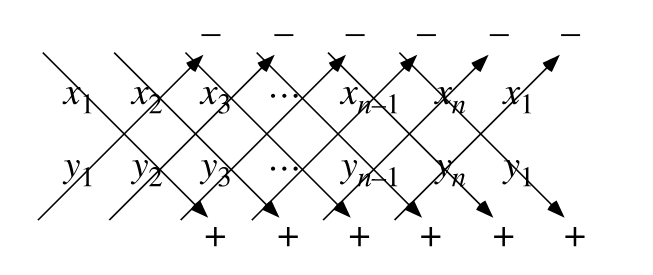

이 공식의 유도와 자세한 정보는 아래의 대단한 분들이 정리를 해놓았다.
https://mathworld.wolfram.com/PolygonArea.html = 가우스 면적 공식에 대해
https://darkpgmr.tistory.com/86 = 다각형 넓이 구하는 방법에 대한 자세한 정보들
https://blog.naver.com/pico0530/221321441913 = 가우스 면적 공식(신발끈 공식)의 유도
정리하면, 점들의 좌표를 받을 때 문제의 범위를 주의하여 (100,000을 제곱해야한다면 10억이 넘어가는 큰 수가 나오므로 일반 int로는 표현이 불가능하다.) 위의 공식에 그대로 대입해주면 된다.
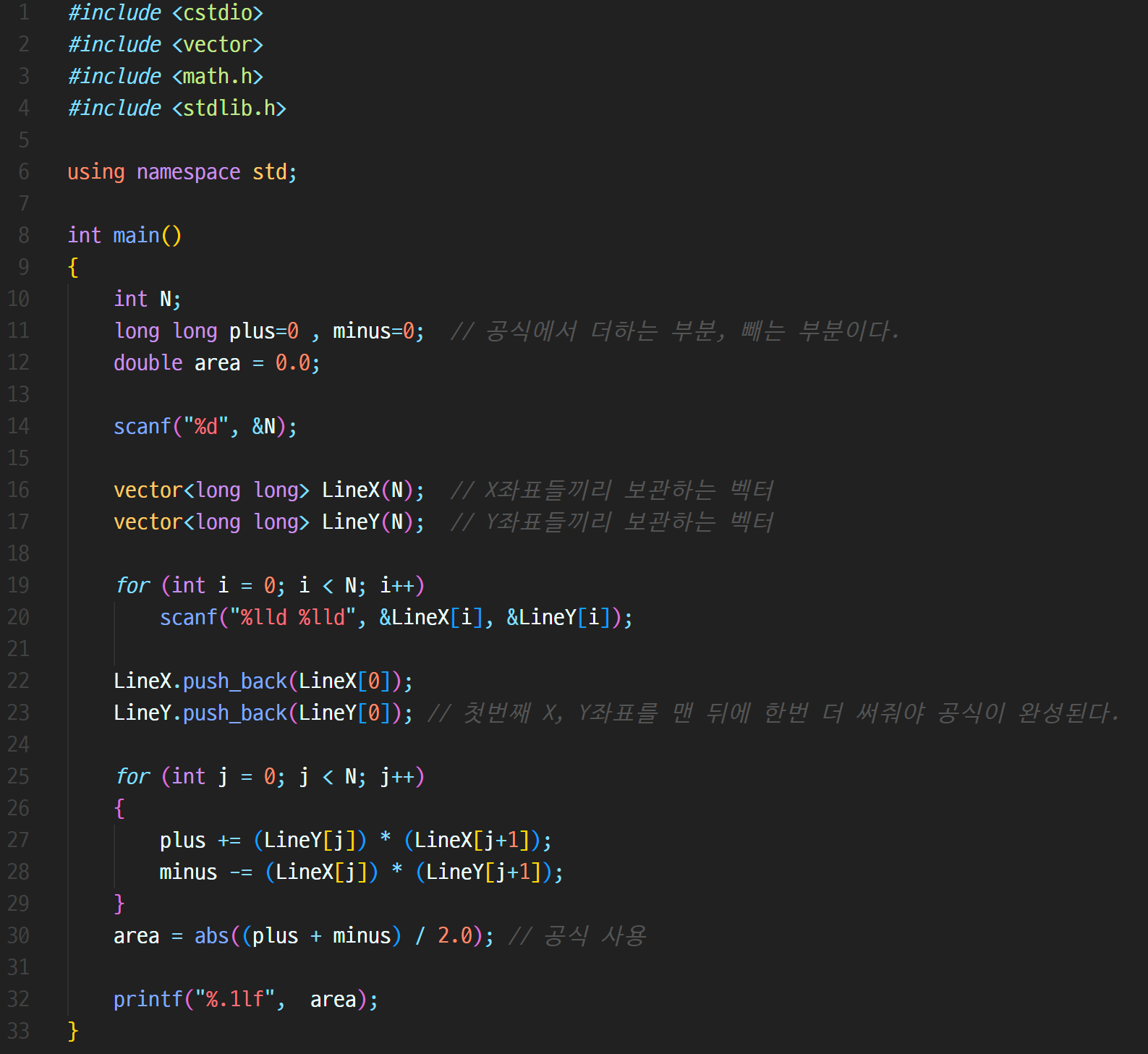
Code
#include <cstdio>
#include <vector>
#include <math.h>
#include <stdlib.h>
using namespace std;
int main()
{
int N;
long long plus=0 , minus=0; // 공식에서 더하는 부분, 빼는 부분이다.
double area = 0.0;
scanf("%d", &N);
vector<long long> LineX(N); // X좌표들끼리 보관하는 벡터
vector<long long> LineY(N); // Y좌표들끼리 보관하는 벡터
for (int i = 0; i < N; i++)
{
scanf("%lld %lld", &LineX[i], &LineY[i]);
}
LineX.push_back(LineX[0]);
LineY.push_back(LineY[0]); // 첫번째 X, Y좌표를 맨 뒤에 한번 더 써줘야 공식이 완성된다.
for (int j = 0; j < N; j++)
{
plus += (LineY[j]) * (LineX[j+1]);
minus -= (LineX[j]) * (LineY[j+1]);
}
area = abs((plus + minus) / 2.0); // 공식 사용
printf("%.1lf", area);
}
Review
필자는 수학을 그다지 좋아하지 않는데, 이런 알고리즘을 풀 때, 수학적 지식이 없으면 그야말로 '노가다'를 해야한다. 수학 그거 배워서 어디 써먹냐고 하는데 이런데 쓴다. 머리가 나쁘면 몸이 고생하듯이, 수학을 모르면 손가락과 머리가 둘다 고생한다.
수학, 꼭 배워 놓으시길...
'오늘의 코드' 카테고리의 다른 글
| 오늘의 코드. 5일차 (백준/2839번 설탕 배달) (2) | 2024.02.08 |
|---|---|
| 오늘의 코드. 4일차 (백준/25642번 젓가락 게임) (4) | 2024.02.07 |
| 오늘의 코드. 3일차 (백준/25305번 커트라인) (1) | 2024.02.07 |
| 오늘의 코드. 2.5일차 (백준/19532번 수학은 비대면강의입니다) (0) | 2024.02.06 |
| 오늘의 코드. 2일차 (백준/10815번 숫자 카드) (0) | 2024.02.06 |
