오늘의 코딩지식. No. 2 (골드바흐의 추측과 소수판별법)

오늘의 코드 6일차 에서 알아본 골드바흐의 추측과 소수판별법에 대해 보다 자세히 정리해 보았다.

 

---

abstarct

우리는 "오늘의 코드. 6일 (백준/9020번 골드바흐의 추측)편"에서 골드바흐의 추측과 소수를 판별하는 여러 아이디어를 다루어 보았다.

 

소수를 판별하는 방식에는 여러가지가 있다. 가장 원초적인 방법부터, 갓 나온 따끈따끈한(비교적으로) 이론들도 여러가지 있다. 간단히 이번 코딩지식의 목차를 크게 나누어 보면 

1. 골드바흐의 추측(Goldbach's conjecture)
2. 소수 판별 - 소수의 성질을 이용한 방법
3. 소수 판별 - 에라토스테네스의 체
4. 소수 판별 -밀러-라빈 소수 판별법 (Miller - Rabin Primality Test)

정도로 추려볼 수 있겠다.

---

Subject - 골드바흐의 추측 (Goldbach's conjecture)

골드바흐의 추측 독일의 수학자 크리스티안 골드바흐가 오일러에게 작성한 한 통의 편지에서 시작한다.

"5보다 큰 모든 정수는 세 소수의 합으로 표현가능하다." - Christian Goldbach

 

이후 편지를 받은 레온하르트 오일러는 다음과 같이 문장을 고쳐썼다.

"2보다 큰 모든 정수는 세 개의 소수의 합으로 표현가능하다." - Leonhard Euler

 

이후 위의 문장이 각각 약한 골드바흐의 추측 (Weak Goldbach conjecture), 아래가 강한 골드바흐의 추측(Strong Goldbach conjecture)으로 현재까지도 수학계의 난제이자 풀리지 않은 철옹성같은 문제로 남아있다.

 

이는 공학계에서도 꽤 큰 화제가 되었고, 가장 최근에는 2013년 해럴드 엘프고트( Harald. A. Helfgott)가 10의 30승 이상의 수의 범위에서 '약한 골드바흐의 추측'이 참이라는 사실을 증명하였고, 여기에 더하여 10의 30승 이전까지의 모든 범위에 대해 "브루트 포스" 알고리즘을 통하여 참 임을 증명하였다. (브루트 포스 알고리즘 : 무차별적으로 모든 경우의 수를 대입하는 알고리즘 = 컴퓨터를 이용한 노가다)

 

혹시 증명 내용이 관심있다면 코넬대학(Cornell Univ.)의 엘프고트의 논문 (Major arcs for GOLDBACH’s problem, H. A. Helfgott, Submitted 13, May, 2013)을 참조해보자. https://arxiv.org/abs/1305.2897

Major arcs for Goldbach's problem

약 80페이지의 기나긴 영어와 기호들이 반겨줄 것이다. (오히려 숫자보다 기호가 많다.)

---

Subject 2 - 소수 판별 - 소수의 성질을 이용한 방법

가장 원초적인 소수를 판별하는 원리이다. 2에서 부터 해당하는 수 N-1의 값까지 나누어 떨어지는 수가 있는지 확인하면 된다. 이는 시간복잡도 O(N)을 가지는 알고리즘으로, 조금 더 발전시켜 약수의 대칭성을 살펴보는 방법이 있다.

 

어떤 수 N이 제곱수라면, √N 을 중심으로 양쪽의 곱이 대칭적이다. 아래에서 예를 들어 N=16이라면

{1, 2, 4, 8, 16} 에서 4를 중심으로 양쪽의 곱 (2 x 8 = 1 x 16) 은 일정하다.

 

그렇다면 굳이 2부터 N까지의 모든 경우를 따져볼 것이 아니라 √N의 약수역시 짝을 갖는다는 점에서 √N의 약수가 존재한다면 소수가 아니며, 존재하지 않는다면 소수로 편별해볼 수 있겠다. 이의 경우, 시간 복잡도는 O(√ N)에 해당한다.

---

Subject 3 - 소수 판별 - 에라토스테네스의 체

이 방법은 어떤 수를 소수인지 판별한다기 보다, 일정 범위 내에서 소수가 얼마나 있고, 어떤 소수가 있는지 알아보는 방법이라고 볼 수 있다.

 

소수의 특징은 1과 자기자신을 제외한 약수가 없다는 점. 그러므로 "소수는 어떤 수의 배수가 될 수 없다(1과 자기자신은 당연히 제외한다.)" 라는 원리를 이용한 방법이다. 이는 이 메커니즘을 고안한 고대 그리스의 수학자이자 천문학자 에라토스테네스(Eratosthenes of Cyrene)의 이름을 따 에라토스테네스의 이름을 따 명명되었다.

 

"소수는 어떤 수의 배수가 될 수 없다" = "모든 수들의 배수들을 제외시면 소수만 남을 것이다. 마치 '체'처럼.

 

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20
21	22	23	24	25

 

다음과 같은 테이블에서 자기자신을 제외한 2의 배수를 제거한다. 다만 1은 소수가 아닌 것으로 생각한다.

	2	3		5
	7		9
11		13		15
	17		19
21		23		25

 

마찬가지로 3의 배수를 제거한다.

	2	3		5
	7
11		13
	17		19
		23		25

 

이를 반복하여 남는 것은 소수뿐이다.

	2	3		5
	7
11		13
	17		19
		23

 

다음과 같은 메커니즘은 O(Nlog(logN)) 시간복잡도를 가진다. 약 100만 정도의 범위의 수에서 주로 사용된다.

---

Subject 4 - 소수 판별 - 밀러 - 라빈 소수 판별법 (Miller - Rabin Primality Test)

이번 포스팅의 하이라이트. 밀러-라빈 소수 판별법이다. 이 방법은 근본적으로 소수임을 엄밀하게 판별할 수 있는 방법은 아니다. 하지만 아득히 먼 천문학적인 수(일반적으로, 적어도 long long 과 같은 어설픈 자료형의 범위는 압도적으로 넘어선다.) 이내에서는 정확한 소수의 판별법이다.

 

이는 페르마의 소정리(Fermat's Little Theorem) = FLT와 합성수를 판단하기 위한 페르마의 인수분해법(Fermat's factorization method) = FF로 불리는 개념들의 이해가 필요하다. 

페르마의 소정리 FLT

이를 통해 다음과 같은 명제 역시 얻어진다.

a ≡ b (mod p) 라는 뜻은 a와 b를 p로 나눈 나머지가 서로 같음을 의미한다. (모듈로 연산)

 

위의 명제에서 만약 이를 만족하는 p가 있다면, 그 p는 소수일 것이다. 다만, 여기서 FLT를 통과하는 일부 합성수들이 존재한다. 그렇다면, 여기서 한번 걸러진 수들에서 합성수를 선택적으로 판별해서 소수인지 아닌지 판단해야 하는데, 이때 FF가 사용된다.

 

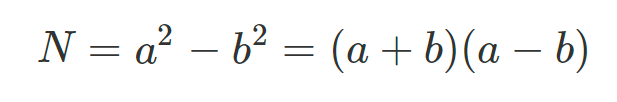
익히 말하는 '합차공식'이 바로 FF의 아이디어의 시작이다. 어떤 수 N을 a제곱 - b제곱꼴로 나타낼 수 있으면 위와 같이 합차의 식으로 분해가 가능하다. 이를 통해 조금 더 발전시켜, (아래부터는 https://www.hostmath.com/의 수식작성 사이트를 이용해 수식들을 직접 그려보며 설명하겠다.)

이를 변형하여,

 

 

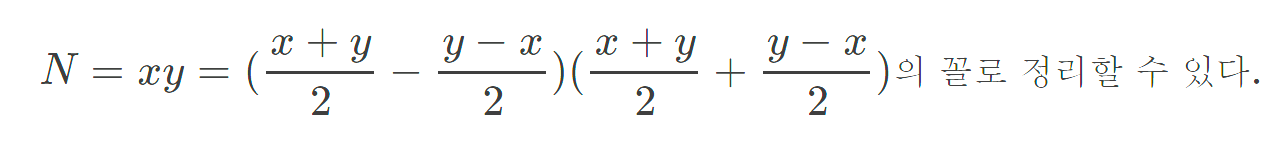
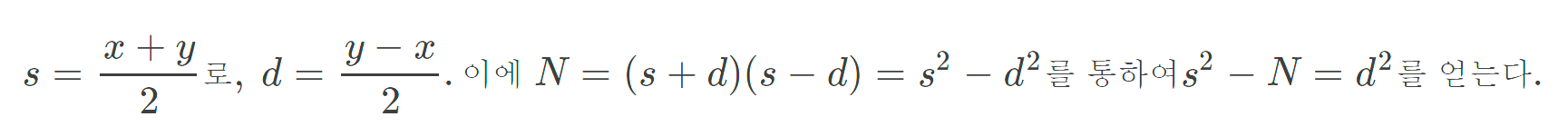
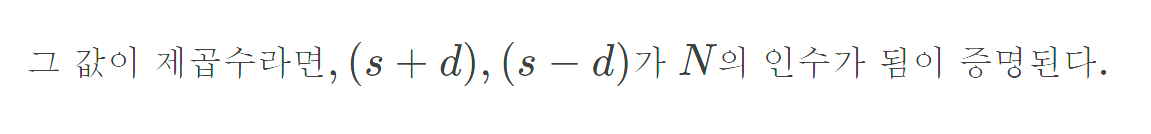
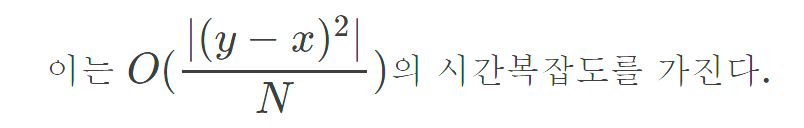
위의 일련의 과정을 정리하면 FLT를 통해 소수로 의심되는 용의자들을 구분해내고, 이를 FF로 합성수인지 소수인지 판단하는 메커니즘이라고 볼 수 있다. 

 

언뜻 상당히 복잡한 알고리즘 같지만, 막상 제곱과 모듈러연산 등이 대부분을 이루는 만큼, 정말 큰 수의 소수 판정에는 꽤 쓸만한 방법이다.

 

---

Conclusion

이번엔 골드바흐의 추측과 소수의 판별에 대해서 알아보았다.

소수 판별시, 사실은 소수의 정의를 이용한 방법과 에라토스테네스의 체 선에서 왠만한 소수들은 판별이 가능하다. 다만 정말 큰수에 있어서는 굉장히 깊은 수준의 수학에 대한 교양이 필요하다.

밀러-라빈 소수판별법에 대해서는 이번 포스트에서 간단한 소개 정도를 하였지만, 혹시나 더 심도 있는 내용이나 코드등을 원한다면 (많지는 않지만) 다양한 내용을 찾을 수 있으니, 꼭 한번 다시 찾아보길 바란다.

큰 소수를 다루는 알고리즘을 짜야한다면, 밀러-라빈 소수판별법이 그 답이 될 것이다.

 

그리고 사실 이런 어려워 보이는 알고리즘도 하나하나 바라보면 생각보다 이해하는데 큰 문제는 없다. 이런 보석같은 알고리즘을 이용하는데는 어쩌면 돈만큼, 돈보다 소중한 끈질긴 인내심과 탐구심이 필요할 것이다.

 

필자도 해당부분에 대해서 100%이해하였냐 라는 물음에는 그렇다고 할 수 없다.

다만, 경험해본 사람과 0에서 부터 시작하는 사람은 확실히 다르다고 생각한다. 그리고, 이런 새로운 개념이 있는지 알려고 노력하는 사람과 그렇지 않은, 우물 안의 개구리는 정말 하늘과 땅차이이다.

 

보다 다양한 분야의 얕은 지식이 더 필요할 것이다. 깊다면 더할나위 없겠지만.

 

"해당 포스팅은 추후 더 다양하고 정리된 내용으로 수정하겠다."