쉽다. (진짜로)
Baekjoon / Problem No. 1037 (약수)
Problem
양수 A가 N의 진짜 약수가 되려면, N이 A의 배수이고, A가 1과 N이 아니어야 한다. 어떤 수 N의 진짜 약수가 모두 주어질 때, N을 구하는 프로그램을 작성하시오.
Input
첫째 줄에 N의 진짜 약수의 개수가 주어진다. 이 개수는 50보다 작거나 같은 자연수이다. 둘째 줄에는 N의 진짜 약수가 주어진다. 1,000,000보다 작거나 같고, 2보다 크거나 같은 자연수이고, 중복되지 않는다.
Output
첫째 줄에 N을 출력한다. N은 항상 32비트 부호있는 정수로 표현할 수 있다.
Solution 1
약수의 특성을 알아보자
- 1은 모든 수의 약수이다.
- 어떤 수의 약수중에서 가장 작은 수는 항상 1이다.
- 어떤 수의 가장 큰 약수는 자기 자신이다.
문제에서 말하는 '진짜 약수' 는 1과 N(자기자신)을 제외했다. (사실 1과 자기자신 역시 약수이므로, 이 문제에서 '진짜 약수'라는 용어를 새로 설정한 것이겠다.)
임의의 수 N에 대하여 원소들을 나열하여 볼때,

다음과 같이 표현된다.
하나의 규칙이라면, 앞에서 n번째 원소와 뒤에서 n번째 원소의 곱은 항상 일정하다.
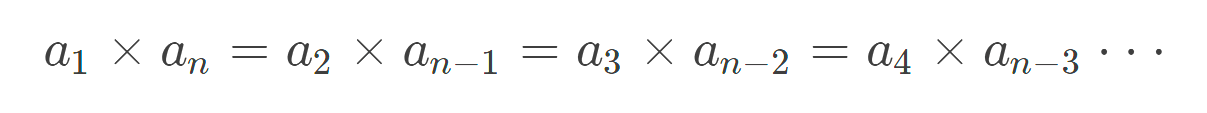
그러면 원소가 랜덤하게 입력된다면, 정렬을 하고 양 끝 값(문제에서 말하는 '진짜 약수'는 1과 N을 포함하지 않으므로 )을곱해주면 문제가 해결될 것이다.
코드를 짜볼까.
Code
#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
int main(void) {
int NumerOfDivisor, Divisors; // 입력받을 약수의 개수, 약수들
scanf("%d", &NumerOfDivisor);
vector<int> num; // N의 '진짜 약수'를 받는 벡터
for (int i = 0; i < NumerOfDivisor; i++) {
scanf("%d", &Divisors);
num.push_back(Divisors);
}
sort(num.begin(), num.end()); // 정렬
printf("%d", num.front() * num.back()); // 앞과 뒤를 곱하여 출력
}
물론 이것보다 짧게 짜는것도 충분히 가능하겠지만, 가독성을 위해 정리해보았다.

Review
정말 쉽다. 솔직히 말해서 분량을 날로 먹으려고 푼게 맞다(?).
양심은 있어서 5.5일차로 올리면서 양심의 가책을 조금이나마 덜어보았다.
'오늘의 코드' 카테고리의 다른 글
| 오늘의 코드. 7일차 (백준/13909번 창문 닫기) (2) | 2024.02.10 |
|---|---|
| 오늘의 코드. 6일차 (백준/9020번 골드바흐의 추측) (1) | 2024.02.09 |
| 오늘의 코드. 5일차 (백준/2839번 설탕 배달) (2) | 2024.02.08 |
| 오늘의 코드. 4일차 (백준/25642번 젓가락 게임) (4) | 2024.02.07 |
| 오늘의 코드. 3.5일차 (백준/2166번 다각형의 면적) (1) | 2024.02.07 |
