알다시피 코딩에서 조합론이란, 시간을 줄이는 싸움이다.
시간 효율성을 높이기 위한 조합론 문제를 찾던 중, 만만해 보이는 녀석을 가져왔다.
Baekjoon / Problem No.1010 (다리놓기)
Problem
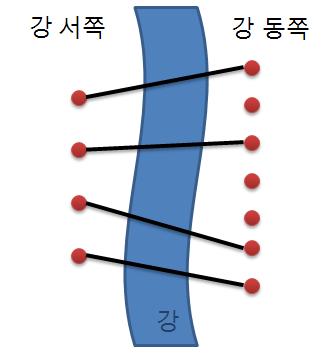
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.
Input
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
Output
각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.
Solution
문제가 하는 이야기를 잘 정리해보면,
- 한 개의 사이트에는 한 개의 다리만 가능 (수학에서의 일대일 대응 관계라고 볼 수 있다.)
- 다리끼리 서로 겹쳐 지을 수 없다. (결국 위의 다리와 아래쪽의 다리가 순서대로 이어져야한다.)
강 서쪽의 사이트들을 한데 묶어 정의역, 동쪽을 공역으로 구분하여
정의역 X를 a, b, c ···로 두어 함수 f를 생각해 볼 때,

라는 것을 확인할 수 있다.
위의 조건이 없다면 단순히 일대일 대응 만을 표현하기 때문에 M개의 동쪽 사이트에서 N개의 서쪽 사이트를 뽑아 하나씩 매칭시키는 것이므로 '순열(Permutation)'을 사용하게 될 것이다.

다만, 조건을 따져서 생각해본다면, 뽑아놓고 조건에 맞게 지정해주는, '조합(Combination)'을 이용할 수 있다.
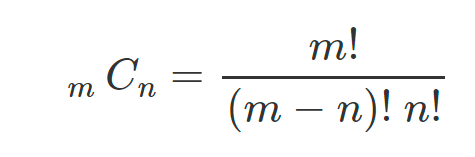
이제 문제는 단순한 분수를 계산하는 것에 지나지 않지만, 문제는 팩토리얼이다. 어떤 수 N 의 팩토리얼은 N이 커지면 기하급수적으로 커지게 된다. 이 문제에서는 사이트의 범위가 30까지의 제한으로 이루어져 있어서 크게 문제는 없다.
여기서 팩토리얼 함수를 따로 만들기 보다는 for반복문을 한개만 써서 m! 과 (m-n)!의 겹치는 부분을 미리 나누어 주고 계산하면 더 바르게 할 수 있겠다.
"위의 큰 수의 팩토리얼은 코딩 지식 게시판의 "오늘의 코딩지식. No. 3 큰 수의 팩토리얼" 편에서 추후에 자세히 다루겠다."
Code
#include <cstdio>
int main()
{
int T;
scanf("%d", &T);
for (int i = 0; i < T; i++)
{
int N, M;
int result = 1;
scanf("%d %d", &N, &M);
int D = 1; // 분모 부분 (denominator)
for (int j = M; j > M - N; j--)
{
result *= j;
result /= D;
D++;
}
printf("%d\n", result);
}
}
위와 같이 안쪽의 for문을 통해 겹치는 부분을 미리 나누어 주는 동시에 분모를 계산까지 해준다면, 조금 더 효율적으로 조합을 계산할 수 있겠다.
Review
설 연휴 때문에 아무래도 '오늘의 코딩지식' 들이 미뤄지고 있다. 끝나는 대로 올릴 예정이니 조금만 기달려주기 바란다. (그때의 필자가 어떻게든 써낼 것이라 믿는다.)
'오늘의 코드' 카테고리의 다른 글
| 오늘의 코드. 10일차 (백준/27960번 사격 내기) (2) | 2024.02.13 |
|---|---|
| 오늘의 코드. 9일차 (백준/1929번 소수 구하기) (2) | 2024.02.12 |
| 오늘의 코드. 7일차 (백준/13909번 창문 닫기) (2) | 2024.02.10 |
| 오늘의 코드. 6일차 (백준/9020번 골드바흐의 추측) (1) | 2024.02.09 |
| 오늘의 코드. 5.1일차 (백준/1037번 약수) (1) | 2024.02.08 |
