인생은 속도가 아니라 방향이다. 여기에서 무언가 끓어오르는(지적하고 싶은) 감정을 느꼈다.
Baekjoon / Problem No. 11758 (CCW)
Problem
2차원 좌표 평면 위에 있는 점 3개 P1, P2, P3가 주어진다. P1, P2, P3를 순서대로 이은 선분이 어떤 방향을 이루고 있는지 구하는 프로그램을 작성하시오.
Input
첫째 줄에 P1의 (x1, y1), 둘째 줄에 P2의 (x2, y2), 셋째 줄에 P3의 (x3, y3)가 주어진다. (-10,000 ≤ x1, y1, x2, y2, x3, y3 ≤ 10,000) 모든 좌표는 정수이다. P1, P2, P3의 좌표는 서로 다르다.
Output
P1, P2, P3를 순서대로 이은 선분이 반시계 방향을 나타내면 1, 시계 방향이면 -1, 일직선이면 0을 출력한다.
Solution 1 - 일차 부등식
우선 문제에 맞게 상황을 여러가지 경우의 수를 따져서 생각해보자.
Case 1 - B가 A기준으로 1사분면인 경우
C1.1 - C는 직선 AB 위에있으면 반시계 방향이다.

C1.2 - C는 직선 AB 아래에있으면 시계 방향이다.
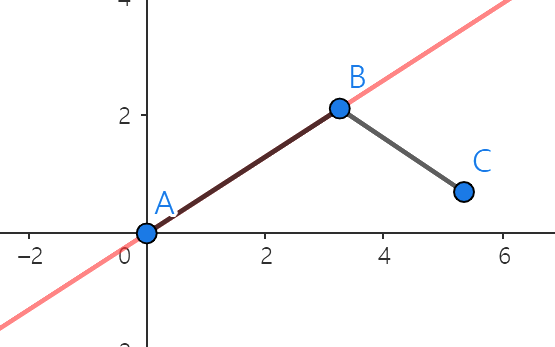
Case 2 - B가 A기준으로 2사분면인 경우
C2.1 - C는 직선 AB 위에있으면 반시계 방향이다.
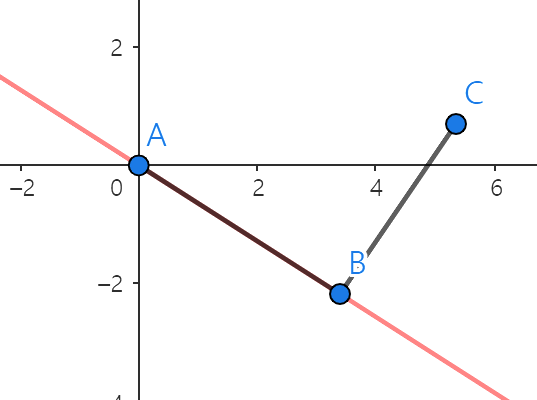
C2.2 - C는 직선 AB 아래에있으면 시계 방향이다.
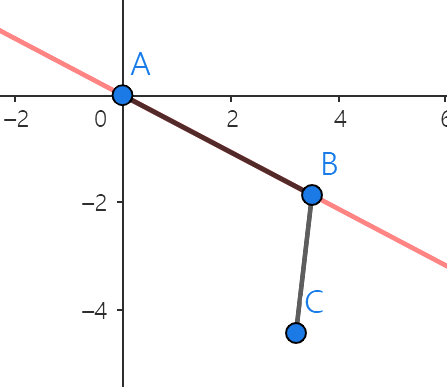
Case 3 - B가 A기준으로 3사분면인 경우
C3.1 - C는 직선 AB 위에있으면 시계 방향이다.
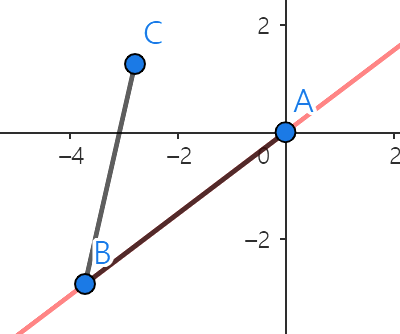
C3.2 - C는 직선 AB 아래에있으면 반시계 방향이다.
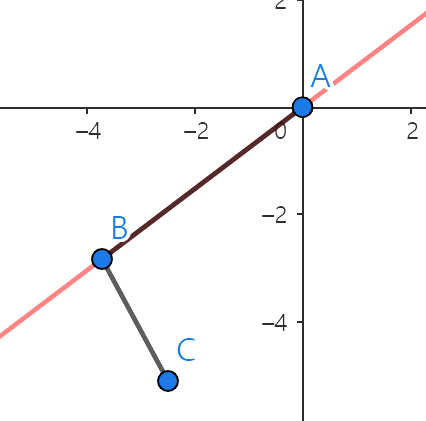
Case 4 - B가 A기준으로 4사분면인 경우
C4.1 - C는 직선 AB 위에있으면 시계 방향이다.

C4.2 - C는 직선 AB 위에있으면 반시계 방향이다.

4개의 상황으로 나누어 봤을때,
B의 X좌표 > 0 일때는 일차식 위에서 반시계, 아래에서 시계방향을 가지며,
B의 X좌표 < 0 일때는 각각 시계, 반시계방향을 가진다.
#include <cstdio>
struct point
{
int x, y;
};
float slope(struct point p1, struct point p2)
{
return (p2.y - p1.y) / (p2.x - p1.x);
}
int main()
{
point A, B, C;
scanf("%d %d", &A.x, &A.y);
scanf("%d %d", &B.x, &B.y);
scanf("%d %d", &C.x, &C.y);
if (slope(A, B) == slope(A, C) && slope(B, C))
printf("0");
else if (B.x > 0)
{
// 1, 2의 경우
}
else if (B.x < 0)
{
// 3, 4의 경우
}
}
이 경우에 위의 코드와 같이 일차부등식의 원리를 이용하여 쉽게 구할 수 있다.
뻥이다. 이런식으로는 (물론 식을 잘 변형한다면 할 수야 있겠지만) 머리가 아프고 손가락이 힘들 뿐이다.
원리는 틀린 것 하나 없다. 다만 우리의 영원한 친구 컴퓨터는 부동소수점을 애매하게 대답해주는 특징이 있다.
식에서 나누는 과정이 생겨나게 되면 부동소수점 표기 오류때문에 문제를 해결하는데 지장이 생긴다.
이를 어떻게 할 수 없을까?
Solution 2 - 벡터의 외적
사실 점 A와 점 B, 점 C의 진행방향을 아는 것이 이 문제의 관건인데,
방향하면 생각나는 것이있다.
"인생은 속도가 아니라 방향이다."
라고 하는 구절을 들으면 이과생들은 당연히 입에 거품을 물 것이다.
속도는 '벡터'량으로, 방향을 가지기 때문이다. 바로 그것이다. 방향하면 벡터가 자동으로 떠오른다. (물론 코딩에서의 벡터와는 다른 개념이다. 기하학에서의 벡터 말이다.)
알다시피, 기하과목을 배운다면, 조금 어려운 문제로 이와 비슷한 문제가 나오게 된다.
시계 방향인지 반시계 방향인지 판별하는 기준(=판별식)은 '벡터의 외적'을 이용한다.
우리가 고등학교 교육과정에서 배운 외적이란, 기호 ⊗로 나타내며,

로 생각하면 된다.
다만, 선형대수학의 버전으로는 조금 다르게 표현한다.
[ 실수공간 Rm, Rn에 각각 정의된 열벡터 a와 열벡터 b에 대하여, ]
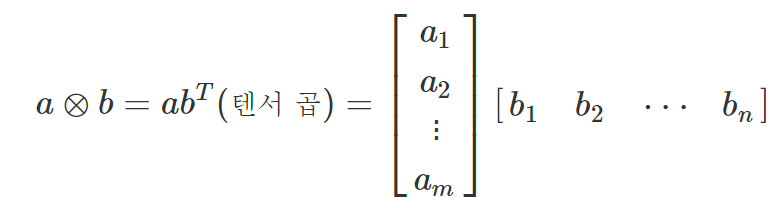
다음을 만족한다.
특히, 외적의 특징(혹은 용례)로써,
벡터 p(점 A와 점 B의 벡터)와 벡터 q의(점 B와 점 C의 벡터) 외적을 D(Discriminant = 판별식) 라고 할때,
- D > 0에서 세 점은 시계방향을 이룬다.
- D = 0에서 세 점은 같은 직선 위에 있다.
- D < 0에서 세 점은 반시계방향을 이룬다.
와 같은 특징을 지닌다.
이를 이용하여 간단히 코드를 작성할 수 있다.
Code
#include <cstdio>
struct point
{
int x, y;
};
int Direction(struct point A, struct point B, struct point C)
{
return (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y);
}
int main()
{
point A, B, C;
scanf("%d %d", &A.x, &A.y);
scanf("%d %d", &B.x, &B.y);
scanf("%d %d", &C.x, &C.y);
if (Direction(A, B, C) == 0)
printf("0");
else if (Direction(A, B, C) > 0)
printf("1");
else if (Direction(A, B, C) < 0)
printf("-1");
}
Review
물론 조건을 다 따져서 충분히 풀 수 있겠다만(기하학적으로는), 부동소수점이라는 코딩쪽의 문제가 겹쳐 조금 귀찮게 된 문제이다.
"인생은 속도가 아니라 방향이다."라는 문장은 사실 이과감수성으로 보았을 때, 그리 매끄러운 말은 아니다.
조금 고쳐보자 한다.
"인생은 속도도 좋지만, 방향으로 충분하다."
바른 방향으로 나아간다고 해도 반드시 최선의 결과로 이어지지 않는다. 안타깝게도 이런 일은 종종 일어난다.
속도가 느리다고 그다지 좌절하지 않았으면 한다. 느리다고 초조해 할 필요도 없다.
최근 여행을 하며 바깥풍경을 바라보곤 한다. 일상이라는 초조한 순간에서 벗어나 느린 시선으로 바라보면,
보이지 않던 것도 보이고, 보였던 것에서 새로운 것을 발견하기도 한다.
굳이 빠를 필요는 없다.
혹시 의외의 순간에 자신이 좋아하는 것을, 잘하는 것을, 또는 자신을 필요로 하는 곳을 찾을지 누가 알겠는가.
마치 벡터연산에서 없어서는 안될 영벡터(0-벡터) 처럼.
'오늘의 코드' 카테고리의 다른 글
| 오늘의 코드. 14일차 (백준/11047번 동전 0) (0) | 2024.02.21 |
|---|---|
| 오늘의 코드. 13일차 (백준/12789번 도키도키 간식드리미) (0) | 2024.02.16 |
| 오늘의 코드. 11일차 (백준/2563번 색종이) (2) | 2024.02.14 |
| 오늘의 코드. 10일차 (백준/27960번 사격 내기) (2) | 2024.02.13 |
| 오늘의 코드. 9일차 (백준/1929번 소수 구하기) (2) | 2024.02.12 |
