2차원 배열을 사용하는간단한 문제이다.
Baekjoon / Problem No. 2536 (색종이)
Problem
가로, 세로의 크기가 각각 100인 정사각형 모양의 흰색 도화지가 있다. 이 도화지 위에 가로, 세로의 크기가 각각 10인 정사각형 모양의 검은색 색종이를 색종이의 변과 도화지의 변이 평행하도록 붙인다. 이러한 방식으로 색종이를 한 장 또는 여러 장 붙인 후 색종이가 붙은 검은 영역의 넓이를 구하는 프로그램을 작성하시오.
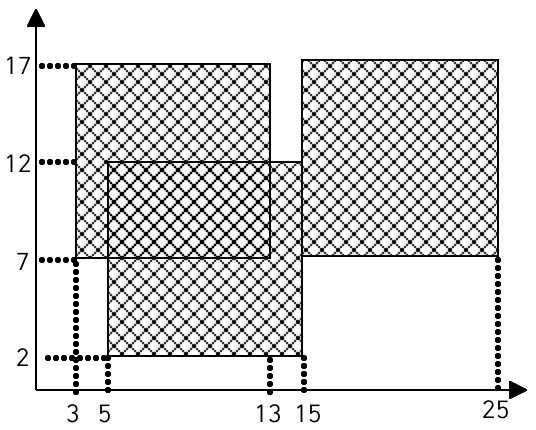
예를 들어 흰색 도화지 위에 세 장의 검은색 색종이를 그림과 같은 모양으로 붙였다면 검은색 영역의 넓이는 260이 된다.
Input
첫째 줄에 색종이의 수가 주어진다. 이어 둘째 줄부터 한 줄에 하나씩 색종이를 붙인 위치가 주어진다. 색종이를 붙인 위치는 두 개의 자연수로 주어지는데 첫 번째 자연수는 색종이의 왼쪽 변과 도화지의 왼쪽 변 사이의 거리이고, 두 번째 자연수는 색종이의 아래쪽 변과 도화지의 아래쪽 변 사이의 거리이다. 색종이의 수는 100 이하이며, 색종이가 도화지 밖으로 나가는 경우는 없다.
Output
첫째 줄에 색종이가 붙은 검은 영역의 넓이를 출력한다.
Solution 1
2차원 배열을 한 폭의 도화지로 생각해보자. (왠지 시적인 표현처럼 보인다.) 각 사각형의 크기는 10x10의 크기를 가지고 있다. 다만 이 사각형들이 중복되는 부분의 넓이는 빼야 한다.
굳이 그렇게 해야할까? 대수적으로 계산을 하려는 순간 머리가 복잡해진다.
문제의 조건은 도화지의 크기는 한변이 100인 정방형이다.
문제를 조금 축소시켜 널이가 10x10인 배열이 있다고 가정해보자.
| ■ | ■ | ■ | |||||||
| ■ | ■ | ■ | |||||||
| ■ | ■ | ■ | ■ | ■ | ■ | ||||
| ■ | ■ | ■ | ■ | ||||||
| ■ | ■ | ■ | ■ | ■ | |||||
| ■ | ■ | ■ | ■ | ||||||
| ■ | ■ | ■ | ■ | ■ | ■ | ■ | |||
| ■ | ■ | ■ | |||||||
| ■ | ■ | ■ | |||||||
다음과 같이 2차원 배열에 겹치는 부분들을 표시해주고, ■를 하나의 단위넓이(1x1)로 취급하여 ■의 개수를 세기만 하면 넓이가 구해진다. 한번 코드로 확인해 보자.
Code
#include <cstdio>
using namespace std;
int Paper[100][100] = {0};
int main()
{
int ColoredPaper; // 색종이의 개수를 받는 변수
int x, y;
int a, b;
int sum = 0; // 넓이의 합계
scanf("%d", &ColoredPaper);
for (int i = 0; i < ColoredPaper; i++)
{
scanf("%d %d", &x, &y);
for (b = 0; b < 10; b++)
{
for (a = 0; a < 10; a++)
Paper[a + x][b + y] = 1; // 마킹
}
}
for (int c = 0; c < 100; c++)
{
for (int d = 0; d < 100; d++)
{
if (Paper[c][d] == 1)
{
sum += 1; // 단위넓이의 합계 계산
}
}
}
printf("%d", sum);
return 0;
}
Review
정말 간단한 문제였다. 다만, 도화지의 크기 등 범위가 바뀌면 2차원 배열을 마킹하는 방식으로는 접근하는 것이 비효율적이므로 또 다른 프로세스를 사용해야할 지도 모른다.
사실 해외여행중이라 정말 간단한 문제를 고르고 고른건 비밀이다. 곧 영양가 높은 컨텐츠로 돌아오겠다.
'오늘의 코드' 카테고리의 다른 글
| 오늘의 코드. 13일차 (백준/12789번 도키도키 간식드리미) (0) | 2024.02.16 |
|---|---|
| 오늘의 코드. 12일차 (백준/11758번 CCW) (2) | 2024.02.15 |
| 오늘의 코드. 10일차 (백준/27960번 사격 내기) (2) | 2024.02.13 |
| 오늘의 코드. 9일차 (백준/1929번 소수 구하기) (2) | 2024.02.12 |
| 오늘의 코드. 8일차 (백준/1010번 다리놓기) (0) | 2024.02.11 |
