이번에야말로 만만해보이는 문제를 고르고 골라왔다.
그래도 양심없이 이걸 하루치로 올리진 않겠다.
Baekjoon / Problem No. 1085 (직사각형에서 탈출)
Problem
한수는 지금 (x, y)에 있다. 직사각형은 각 변이 좌표축에 평행하고, 왼쪽 아래 꼭짓점은 (0, 0), 오른쪽 위 꼭짓점은 (w, h)에 있다. 직사각형의 경계선까지 가는 거리의 최솟값을 구하는 프로그램을 작성하시오.
Input
첫째 줄에 x, y, w, h가 주어진다.
Output
첫째 줄에 문제의 정답을 출력한다.
Solution 1
우선 한눈에 들어오도록 그림으로 그려보자 (GeoGebra 계산기를 사용하였습니다.)

위 그림과 같이 한수는 직사각형 속에 갇혀있다.
과연 어디로 나가야 최단거리로 경계에 도착할 수 있을까?
우선 직선이어야 한다.
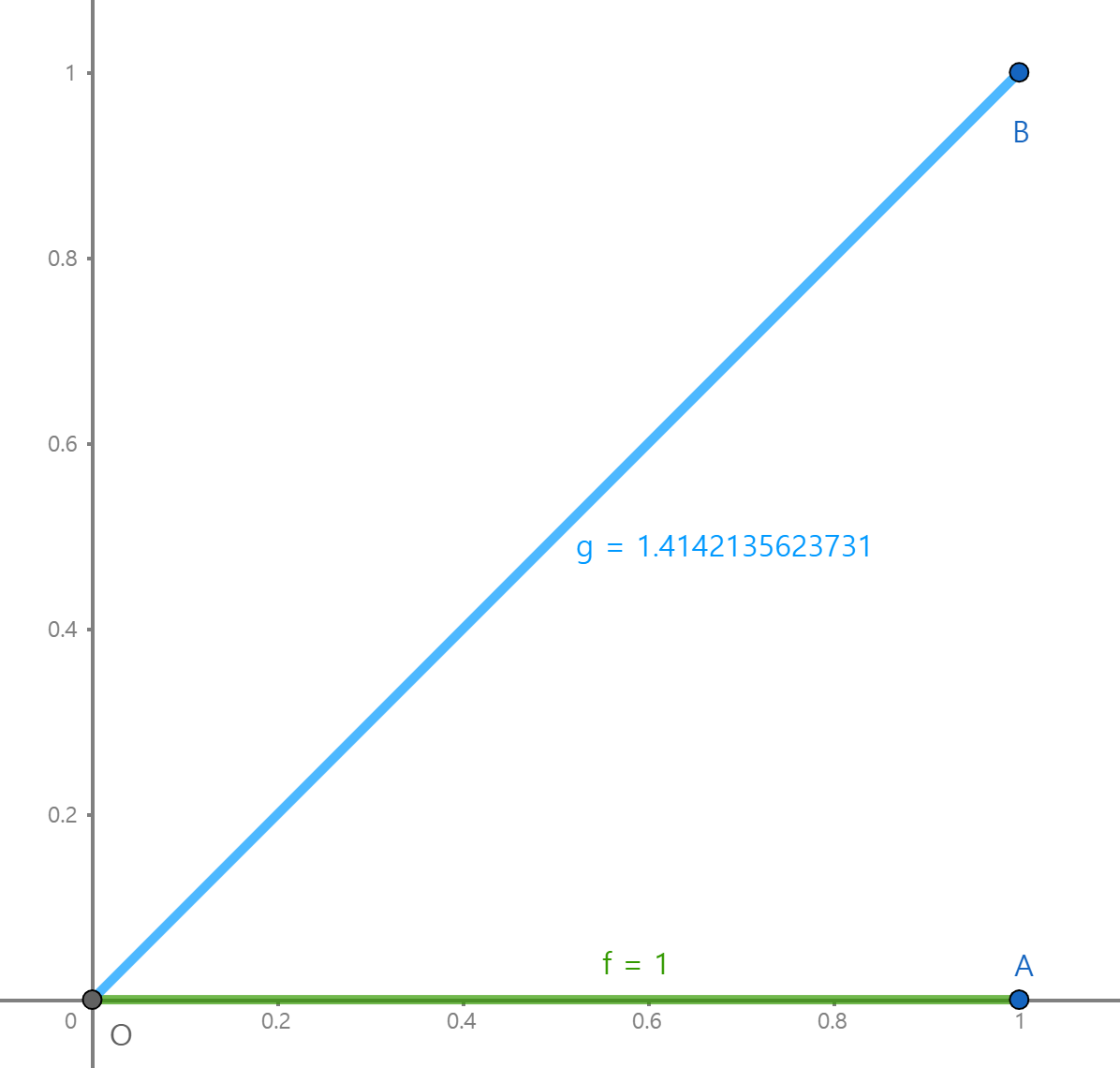
위 그림에서 볼 수 있듯 직선 f (직선거리)와 직선 g(대각선거리)를 비교해보면 대각선 길이가 길다.
그렇다면 한수는 직선거리중 어느 경계면쪽의 직선거리가 가장 짧은지 따져보면 될것이다.
그리하여 한수의 위치를 X성분과 Y성분으로 나누어 보자. (이 표현이 정확한지는 모르겠다.)

위 그림을 볼때 " X성분 1, X성분 2, Y성분 1, Y성분 2 " 중에서 가장 짧은 거리를 찾는 것이 해결방법이겠다.

이를 실제 길이에 대한 식으로 나타내보면 ( x, y, w - x, h - y )이므로 이들중 최솟값을 찾을 수 있다.
드디어 한수는 직사각형으로부터 도망칠 수 있게 되었다.
Code
#include <stdio.h>
int main()
{
int x, y, w, h;
int x1, x2, y1, y2; // X성분 1, X성분 2, Y성분 1, Y성분 2
int min; // 최솟값 비교에 사용
scanf("%d %d %d %d", &x, &y, &w, &h);
x1 = x;
x2 = w - x;
y1 = y;
y2 = h - y;
min = (x1 < x2) ? x1 : x2; // 삼항 연산자를 사용, 비교
min = (min < y1) ? min : y1;
min = (min < y2) ? min : y2;
printf("%d", min);
// 한수 (은)는 무사히 도망쳤다...
}
Review
사실 아이디어 자체는 크게 어렵지 않았다.
다만 코드를 짜는 과정에서 조건문과 반복문 등을 생각해 볼 수 있는데, 간단한 비교라면 삼항연산자 쪽이 더
효율적이다. (코드 길이로 보나 시인성으로 보나) 어찌보면, 난잡하게 조건문, 반복문을 반복하여 쓰는것 보단
효율적이고 간단하게, 보기 쉽게 문제를 풀 수 있는 능력이 앞으로 코딩을 하면서 꼭 필요하지 않을까?
'오늘의 코드' 카테고리의 다른 글
| 오늘의 코드. 3일차 (백준/25305번 커트라인) (1) | 2024.02.07 |
|---|---|
| 오늘의 코드. 2.5일차 (백준/19532번 수학은 비대면강의입니다) (0) | 2024.02.06 |
| 오늘의 코드. 2일차 (백준/10815번 숫자 카드) (0) | 2024.02.06 |
| 오늘의 코드. 1일차 (백준/2869번 달팽이는 올라가고 싶다) (3) | 2024.02.05 |
| 오늘의 코드. 0일차 (Prologue) (2) | 2024.02.04 |
